S2TUL: A Semi-Supervised Framework for Trajectory-User Linking

( , & al., , , , & (). S2TUL: A Semi-Supervised Framework for Trajectory-User Linking. ACM. https://doi.org/10.1145/3539597.3570410 ) 提出了轨迹-用户匹配问题的半监督方法。

数据集：Foursquare

作者给出了预处理好的一个数据集。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

train_trajs.txt: 每一行[User_id, loc_1, loc_2, ..., loc_l]，其中第i个location用一个数字loc_i表示
val_trajs.txt
test_trajs.txt

train_trajs_time.txt: 每一行[t_1, t_2, ..., t_l]，每个t_i为时间戳
val_trajs_time.txt
test_trajs_time.txt

vidx_to_latlon.txt: loc_i到经纬度的映射，用于计算实际的点的距离

vocabs_dict.txt

构图

Repeatability Graph

有相交的两条轨迹之间应该连一条边

首先，直接构建$A_{tl}\in \mathbb{R}^{N_t\times N_l}$，其中$N_t,N_l$分别表示轨迹的数量和最大的loc值。 接着，Repeatability Graph构造为

$$A_R=A_{tl}A_{tl}^T\in\mathbb{R}^{N_t\times N_t}$$

$A_R$中不再含有轨迹中具体的点信息，$A_R$的每个顶点表示一条轨迹。

Spatial Graph

对于两条轨迹$T_1=((l_{11},t_{11}),(l_{12},t_{12}),\cdots,),T_2=((l_{21},t_{21}),(l_{22},t_{22}),\cdots,)$，如果存在一个loc_i和loc_j，使得$d(l_{1i},l_{2j})<\epsilon_s$，那么$T_1,T_2$之间应该连一条边。

构建$A_{ll}\in\mathbb{R}^{N_l\times N_l}$，其中$A_{ll}[i,j]=1$表示第$i$个loc和第$j$个loc的距离小于给定的阈值。接着，Spatial Graph构造为

$$A_S=A_{tl}\tilde{A}_{ll}A_{tl}^T\in\mathbb{R}^{N_t\times N_t}$$ 其中$\tilde{A}_{ll}$将$A_{ll}$的对角线值改为0。

对于$A_{tl}[i,:]$，即第$i$条轨迹的one-hot向量，$A_{ll}[:,j]$表示和loc_j距离相近的邻居点的one-hot向量，二者内积得到$A_{tl}\tilde{A}_{ll}[i,j]$的值，表示将第$i$条轨迹的第$j$个location的值修改为loc_j的邻居个数（如果轨迹$i$中包含loc_j）。最后的$A_{tl}^T$用于匹配，即仍然要根据两条轨迹的匹配程度连边和加边权。

Spatial-Temporal Graph

对于两条轨迹$T_1=((l_{11},t_{11}),(l_{12},t_{12}),\cdots,),T_2=((l_{21},t_{21}),(l_{22},t_{22}),\cdots,)$，如果存在一个loc_i，使得$d(l_{1i},l_{2j})<\epsilon_s$同时$d(t_{1i},t_{2j})<\epsilon_t$，那么$T_1,T_2$之间应该连一条边。

对于Spatial Graph中的每一条边，验证它们是否同时满足时间戳的相近性。需要注意由于定义轨迹的邻近性时都使用了存在性定义，而ST邻近性要求空间邻近和时间邻近在一个点同时满足，因此对于空间邻近的两条轨迹，需要重新验证每一对点之间是否满足空间邻近性。若满足空间邻近性，才能继续考察时间邻近性。

组合图信息

将Spatial Graph和Spatial-Temporal Graph分别与Repeatability Graph组合，并使用不同的edge_type区分，得到异构图。

模型

图表征模块

依据输入图是否异构选择GCN或RGCN。

LSTM模块

轨迹是一种单向的线图，可以视作语言数据中的句子，轨迹中的每个顶点视作一个单词。 构造的图中的顶点都没有初始表征，因此作者考虑用LSTM得到每条轨迹的初始表征。

分类器

分类器使用简单的前馈网络。损失函数使用交叉熵。

$$\mathcal{L}=-\sum_{i=1}^{N_t}\sum_{k=1}^{N_u}y_i^t[k]\log y_i[k]$$

其中带$t$表示是ground_truth的one-hot向量。

推理时的小细节

由于一个人在同一时间不能处于两个位置，因此如果两条轨迹都想连接到同一个用户，且轨迹在同一时间戳有两个不同的位置点，那么就只能选择其中一条轨迹连接到该用户。

作者将测试集所有轨迹对所有用户的预测结果根据预测分数进行排序。先将分数高的轨迹连接到用户，后面遇到冲突时直接跳过，直到找到每条轨迹对应的用户。

实验

本文将TUL问题建模为多分类问题。评估参量有

  • $ACC@K_a$：如果真实用户出现在排好序的前$K_a$个分数中，$ACC@K_a=1$
  • Macro-P,Macro-R,Macro-F1：分别表示每个用户上的precision,recall,F1的平均值。例如，

$$\text{Macro-F1}=\frac{\sum_{i=0}^{N_u}F1_i}{N_u}$$

实验结果显示使用LSTM并不会一直得到最优的预测准确度。

Contrastive Pre-training with Adversarial Perturbations for Check-in Sequence Representation Learning

( , & al., , , , , , , & (). Contrastive Pre-training with Adversarial Perturbations for Check-In Sequence Representation Learning. Proceedings of the AAAI Conference on Artificial Intelligence, 37(4). 4276–4283. https://doi.org/10.1609/aaai.v37i4.25546 ) 提出了使用对比学习预训练的方法。作者认为现有对比学习方法的数据增强方法不适用于轨迹数据，因为他们做的数据扰动在具有地理和时间信息的数据中是无意义的，无法给模型提供真正需要学习的困难样本。因此，本文提出利用对抗方法提供时间-地理数据的数据增强和难样本。

数据定义

一个“签到”序列被定义为$T=(r_1,r_2,\cdots,r_n)$，其中$r=(t,p)$在时间戳$t$时出现在位置$p\in P$。POI点集$P$中的每个点$p$都有唯一的经纬度和语义信息。

本文首先设计预训练模型$G$学习序列中每个位置的表征：$G(T)$。接着，将表征用于下游分类预测任务，如位置预测（Location Prediction, LP）和轨迹用户匹配（Trajectory User Link, TUL）。

轨迹数据的表征学习

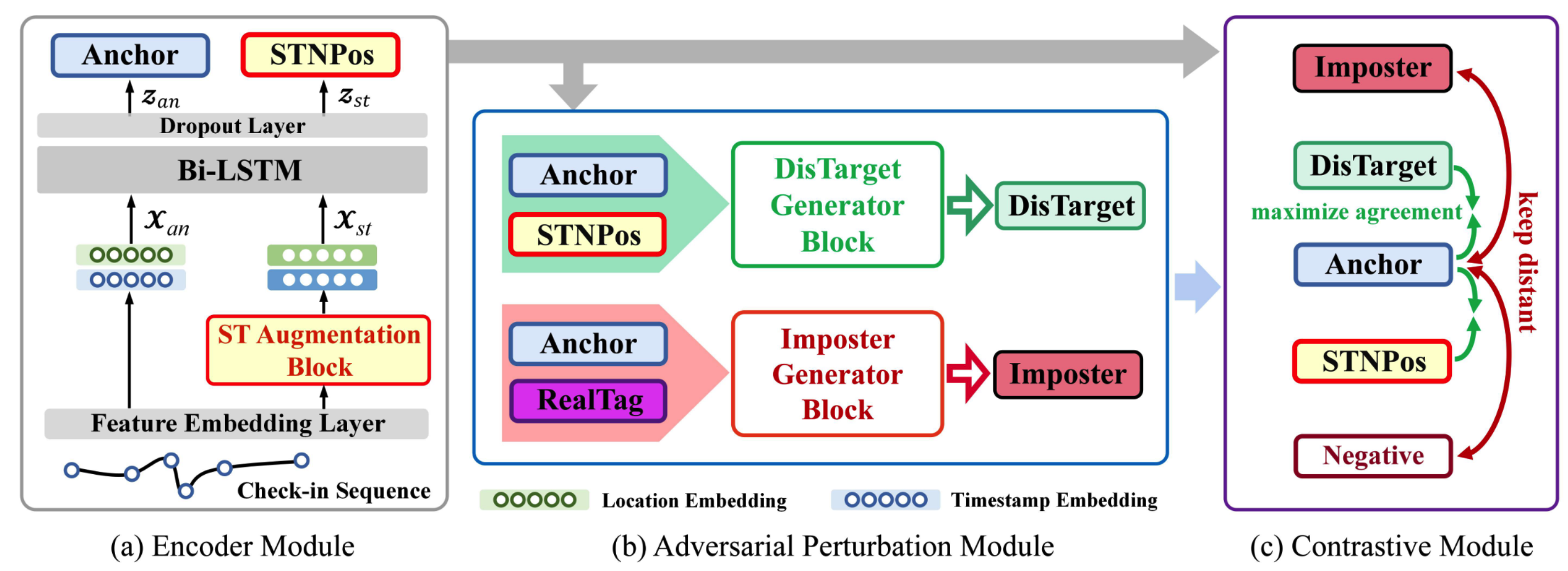
在进入模型前，作者首先将每个POI位置表示为$|P|$维的独热编码。将时间戳划分到24小时中的某一小时，接着使用24维的独热编码作为时间戳的初始表征。表征模型将POI映射到向量$E_p\in \mathbb{R}^{|P|\times d_p}$，将时间戳映射到向量$E_t\in \mathbb{R}^{24\times d_t}$。 上述表征学习记为$X=(x_1,\cdots,x_n)=f(T;\theta_{st})$。作者未说明$E_p,E_t$和$X$的关系。 接着，将表征$X$输入双向LSTM，即BiLSTM，用于建模签到序列中的语义信息。将最后的隐藏态$h_n\in\mathbb{R}^{2d}$作为序列的最终表征$z$。其中，$h_n$由两个方向的最终态$\overleftarrow{h_n},\overrightarrow{h_n}\in\mathbb{R}^{d}$拼接而来。

轨迹数据的增强和难样本生成

将上述表征记作锚点表征$X_{an}=f(T;\theta_{st})$。为了得到正样本，作者使用高斯噪声对表征模型的权重参数进行扰动，得到正样本$X_{st}$：

$$ \begin{align} X_{st}&=f(T;\theta_{st}’) \\ \theta_{st}’&=\theta_{st}+\eta\Delta\theta_{st} \\ \Delta\theta_{st}&\sim \mathcal{N}(0,\sigma^2) \end{align} $$

作者将正样本称为时空噪声正样本（spatial temporal noise positive, STNPos）。经过相同的LSTM得到的序列的表征相对应的锚点和正样本分别记作$z_{an},z_{st}$。

难样本生成

对于序列中的任意一个点$z_{an}$，将它在序列中的下一个点当作标签，那么负样本$z_{im}$首先考察距离$z_{an}$较近，但最不可能的下一个点，即

$$ \begin{align} z_{im} &= z_{an}-\epsilon\frac{g}{\parallel g\parallel_2} \\ g &= \nabla_{z_{an}}\log p_{\theta}(y|X_{an}) \end{align} $$

同理，考察距离$z_{an}$较远，但确实属于序列数据的“语义”的正样本。

最终，正负样本各包含难易两类，如下图所示。

Trajectory-User Linking via Hierarchical Spatio-Temporal Attention Networks

( , & al., , , , & (). Trajectory-User Linking via Hierarchical Spatio-Temporal Attention Networks. https://doi.org/10.48550/arXiv.2302.10903 ) 中设计了新的建图方法，并将轨迹表征器由LSTM替换为注意力模型。

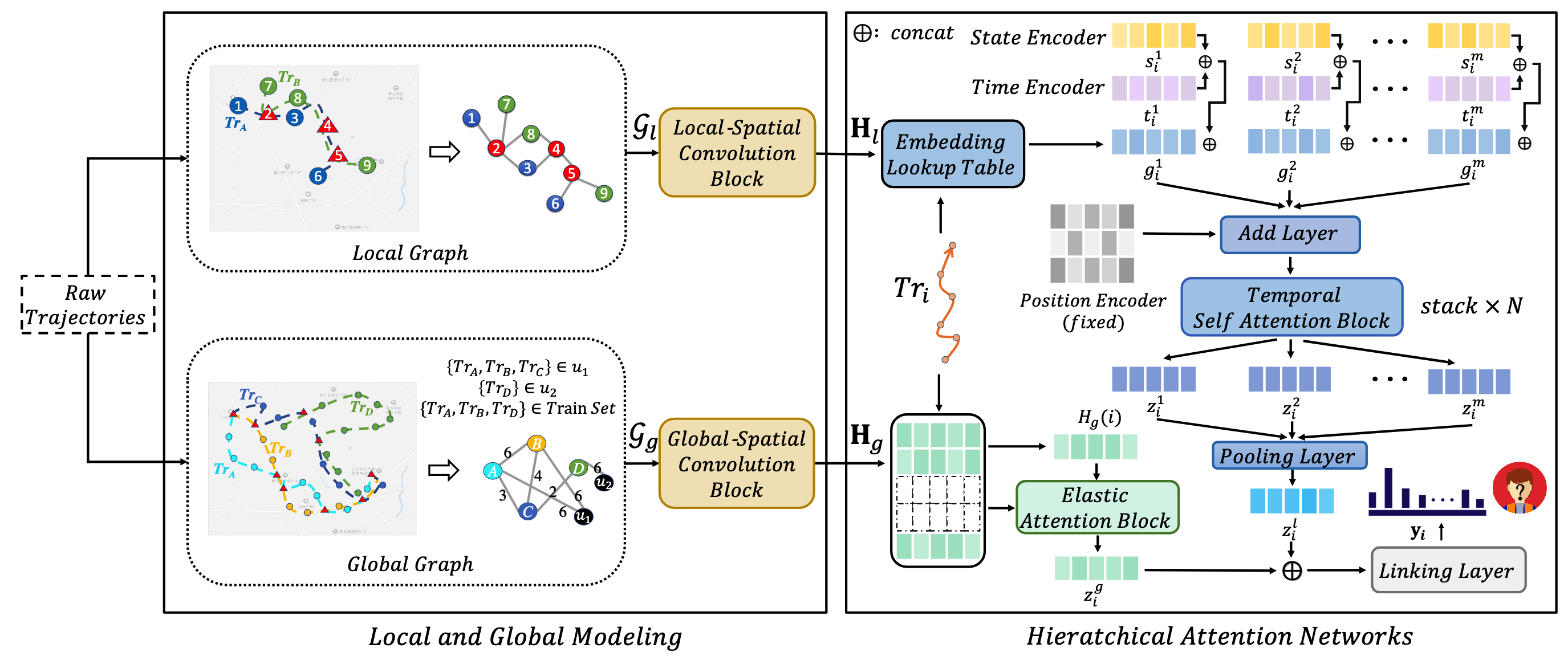
建图方法

作者首先将空间划分为更粗糙的网格区域，将轨迹中每个位置映射到相应的网格：$f_g:l_i\to g_i$。这样，原始轨迹中的每个点$(t_i,l_i)$变为$(t_i,g_i)$。

建立局部空间图

局部空间图中的顶点表示网格位置，如果有轨迹从一个网格直接一步到另一个网格，那么两个网格间连一条边。边上的权重等于符合条件的轨迹数量。不考虑同一网格内的连边，即没有自环。 为每个网格使用独热编码（维度为网格的数量）构建初始特征向量。

建立全局空间图

全局空间图中的顶点有两类：用户和轨迹。如果两个轨迹有相交的网格位置，那么轨迹顶点之间连一条边，边上的权重等于相交网格位置的个数。 同时，轨迹和它们的标签用户之间连边，边上的权重等于该用户的所有轨迹之间连边权重最大值。同样，为每个用户顶点和轨迹顶点构建multi-hot编码，作为初始特征向量。

表征学习

首先使用构建的两种图分别得到初始表征：

  • 使用GCN将局部空间图的顶点（网格位置）映射到表征向量$H_l$
  • 使用GCN将全局空间图的顶点（轨迹和用户）映射到表征向量$H_g$（注：用户表征好像一直没有用上）

位置级别建模

除了由GCN生成的表征向量$H_l$，作者进一步考虑其他附加语义信息，进行表征后拼接到现有表征上。轨迹中的每个位置关联着速度、方向、时间戳等信息，作者使用查表表征模块（torch.nn.Embedding）分别进行表征。这样得到每个网格位置的表征$X_i$。

接着，为了建模长轨迹中的依赖（类似于建模长文本），不同于以往工作采用RNN，本文使用了Transformer解决长时依赖问题。首先定义所有位置共享的位置表征$P$，接着，每个位置的表征向量成为

$$M_i=X_i+P$$

经过Transformer后，得到一条轨迹中每个位置的表征$Z_i=(z_i^1,z_i^2,\cdots,z_i^m)$，再经过一个池化层得到轨迹的表征$z_i^l=\text{Pooling}(z_i^1,z_i^2,\cdots,z_i^m)$。

轨迹级别建模

另一方面，对于有GCN得到的初始轨迹表征$H_g$，作者首先计算每对轨迹之间的余弦相似度，接着利用该相似度更新每条轨迹的表征，具体如下：

$$ \begin{align} a_{i,j}&=\frac{H_g(i)H_g(j)^T}{\parallel H_g(i)\parallel \parallel H_g(j)^T \parallel} \\ A_i&=\{a_{i,1},a_{i,2},\cdots,a_{i,\text{Tr}}\} \\ W^g_i&=\text{Sparsemax}(A_i) \\ z_i^g&=W_i^gH_g \\ \end{align} $$ 其中$\text{Tr}$表示轨迹的个数。

轨迹-用户匹配预测

将上述得到的两种轨迹表征$z_i^l,z_i^g$进行拼接，输入全连接层进行多分类预测。损失函数为标准的交叉熵和正则项的求和：

$$ L(\Theta)=-\frac{1}{\zeta}\sum_{i=1}^{\zeta}y_i\log(\sigma(\hat{y}_i))+\frac{\lambda}{2}\parallel \Theta\parallel^2 $$ 其中$\Theta$表示模型的可训练参数，$\sigma$表示softmax函数，$\zeta$表示训练轨迹的条数，$y_i,\hat{y}_i$分别表示轨迹$i$的真实用户和预测用户。