现实中图的结构可能是不完整或有噪声的。为了在图结构不可靠的情况下较好地完成下游任务，研究者提出了如下的图结构学习算法。

Towards Unsupervised Deep Graph Structure Learning

论文链接： ( , & al., , , , , & (). Towards Unsupervised Deep Graph Structure Learning. https://doi.org/10.48550/arXiv.2201.06367 )

相关工作 - 深度图结构学习

一些传统机器学习算法，如图信号处理，谱聚类，图论等可以解决图结构学习问题。但这类方法往往不能处理图上的高维属性。

最近的深度图结构学习方法用于提升GNN在下游任务上的性能。它们遵循相似的管线：先使用一组可学习的参数建模图的邻接矩阵，再和GNN的参数一起针对下游任务进行优化。基于图结构离散的特性，有多种建模图结构的方法。

  • 概率模型：伯努利概率模型、随机块模型
  • 度量学习：余弦相似度、点积
  • 直接使用$n\times n$的参数矩阵建模邻接矩阵

问题定义

给定输入图$G=(V,E,X)=(A,X)$，$|V|=n,|E|=m,X\in\mathbb{R}^{n\times d}$

  • 结构推理问题：输入信息只有顶点特征矩阵$X$
  • 结构修改问题：输入信息包含了$A,X$，但$A$可能带有噪声

解决方案 - SUBLIME

SUBLIME ( , & al., , , , , & (). Towards Unsupervised Deep Graph Structure Learning. https://doi.org/10.48550/arXiv.2201.06367 ) 将学习到的图结构视作一种数据增强，与原图进行多视角的对比学习。

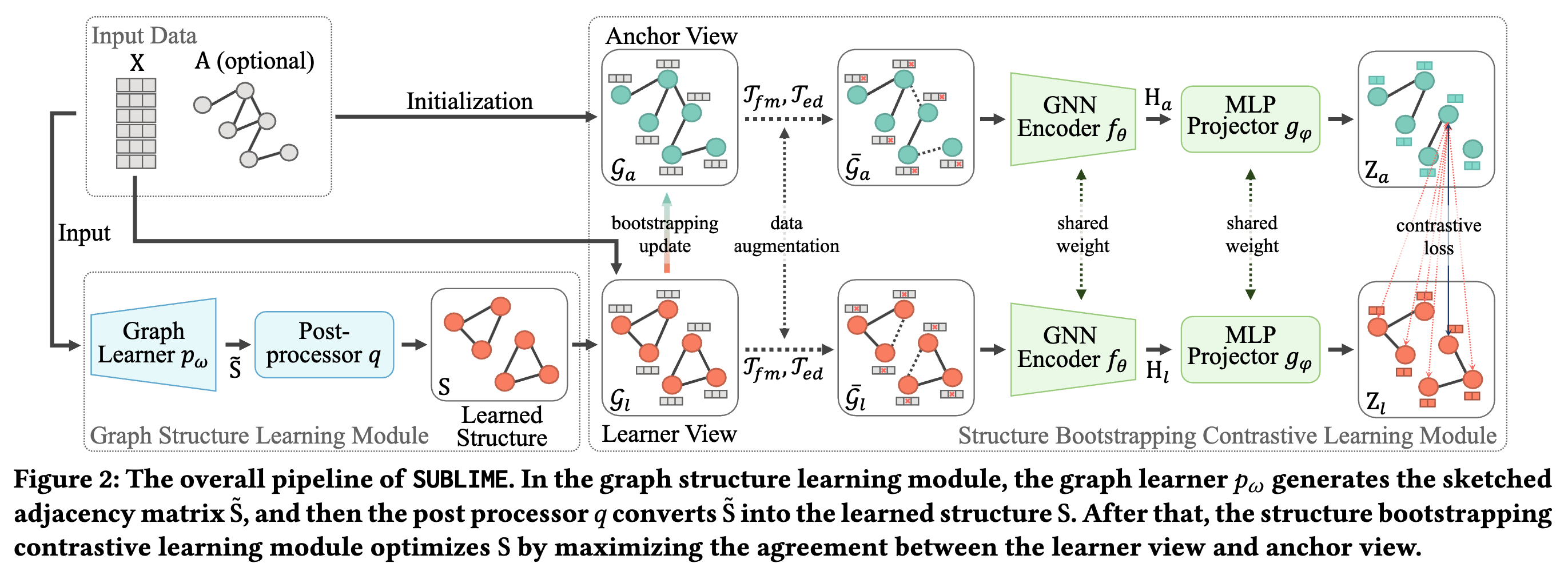
  • 锚点视角（教师）：对于输入带有邻接矩阵$A$的结构修改任务，直接使用输入的$A$作为锚点；对于输入不带邻接矩阵的结构推理任务，使用单位矩阵$I$作为锚点。节点特征使用输入特征$X$。
  • 结构学习器视角（学生）：使用结构学习器的输出作为该视角。节点特征使用输入特征$X$。

SUBLIME定义了四种图结构学习器，使用时需要当作超参数调节：

  • 全图参数化学习器FGP：顾名思义，直接使用一个$n\times n$的参数矩阵作为学习的邻接矩阵，即$S=\sigma(\Omega)$，$\Omega\in\mathbb{R}^{n\times n}$；

    • 初始化：使用节点特征的$k$最近邻初始化$\Omega$。github link

  • 度量学习学习器：先通过输入得到节点的表征$E\in\mathbb{R}^{n\times d}$，再由表征构建学习的邻接矩阵：

$$S=\phi(h_w(X,A))=\phi(E)$$

其中$\phi$是非参数函数（即不用训练的函数），如余弦相似度、闵可夫斯基距离（Minkowski distance）等；$h_w$是表征网络。SUBLIME提供了3种得到$E$的表征方法：注意力学习器、MLP学习器和GNN学习器：

  • 注意力学习器：$E^{(l)}=h_w^{(l)}(E^{(l-1)})=\sigma([e_1^{(l-1)}\odot w^{(l)},\cdots,e_n^{(l-1)}\odot w^{(l)}])^T$，其中$E^{(l)}\in\mathbb{R}^{n\times d}$表示第$l$层表征网络的输出；$e_i^{(l-1)}\in\mathbb{R}^d$表示$E^{(l-1)}$的第$i$行，$w^{(l)}\in\mathbb{R}^d$为权重向量。初始时$E^{(0)}=X$。可以看到该表征学习器没有对特征进行降维，每一层的输出$E$的维度都是$\mathbb{R}^{n\times d}$。

    • 初始化：$w^{(l)}$初始为全$1$向量，即$w^{(l)}=\{1,1,\cdots,1\}\in\mathbb{R}^d$。github link

  • MLP学习器：$E^{(l)}=h_w^{(l)}(E^{(l-1)})=\sigma(E^{(l-1)}\Omega^{(l)})$，其中$\Omega^{(l)}\in\mathbb{R}^{d\times d}$是参数矩阵。

    • 初始化：$\Omega$初始时为单位矩阵。github link

  • GNN学习器：$E^{(l)}=h_w^{(l)}(E^{(l-1)})=\sigma(\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2}E^{(l-1)}\Omega^{(l)})$，其中$\Omega^{(l)}\in\mathbb{R}^{d\times d}$是参数矩阵。

    • 初始化：$\Omega$初始时为单位矩阵。github link

图学习器得到的$S$是全连接的，且不一定对称，所以需要进行后处理：即稀疏化、对称化和正则化。

  • 稀疏化采用$k$最近邻方法，对每个顶点只保留最近的$k$的邻居。
  • 对称化：$S^{sym}=(\sigma(S)+\sigma(S)^T)/2$，其中$\sigma$是ReLU或ELU函数，保证$S’$内的元素都是非负数。
  • 正则化：为保证边权都位于$[0,1]$范围，使用常用的图正则方法：$S’=\tilde{D}^{-1/2}\tilde{S}^{sym}\tilde{D}^{-1/2}$。

得到两个视角的图（锚点视角和学习器视角）后，SUBLIME对每个视角做进一步的数据增强，包括特征扰动和边的扰动。接着，使用GNN编码器（这里使用GCN）将两个视角的图映射到欧氏空间，再使用MLP进一步映射，在MLP的输出上使用节点级别的对比学习损失函数，即最大化同一节点在两个视角图之间的互信息：

$$\begin{aligned}\mathcal{L} &=\frac{1}{2n}\left[l(z_{l,i},z_{a,i})+l(z_{a,i},z_{l,i})\right]\\ l(z_{l,i},z_{a,i}) &= \log\frac{\exp(\cos(z_{l,i},z_{a,i})/t)}{\sum_{k=1}^n\exp(\cos(z_{l,i},z_{a,k})/t)}\end{aligned}$$

其中$t$是温度超参数。

除了使用梯度下降更新参数外，SUBLIME在每个epoch使用bootstrapping更新锚点视角的图结构，以减少噪声和过拟合的影响：

$$A_a\gets \tau A_a+(1-\tau)S$$

其中$A_a$是锚点视角图的邻接矩阵，$S$是图结构学习器输出的图结构。$\tau\in\{0.999,0.9999,0.99999\}$。github link

SLAPS: Self-Supervision Improves Structure Learning for Graph Neural Networks

论文链接： ( , & al., , & (). SLAPS: Self-Supervision Improves Structure Learning for Graph Neural Networks. https://doi.org/10.48550/arXiv.2102.05034 )

问题定义

本文未考虑输入的图结构，只考虑利用输入的节点特征学习图结构。

解决方案 - SLAPS

SLAPS包含4个模块：生成器、邻接关系处理器、分类器和自监督。

生成器

生成器是由节点特征到邻接矩阵的映射：$\mathbb{R}^{n\times d}\to\mathbb{R}^{n\times n}$。SLAPS给出了两种生成器：

  • 全参数FP：使用$n^2$个参数直接表示邻接矩阵
  • MLP-$k$NN：$\tilde{A}=kNN(MLP(X))$，其中MLP：$\mathbb{R}^{n\times d}\to\mathbb{R}^{n\times d’}$；$k$NN：$\mathbb{R}^{n\times d’}\to\mathbb{R}^{n\times n}$

SLAPS初始化两种生成器使其生成$A^{kNN}$，即由输入节点特征$X$计算的$k$最近邻邻接矩阵。对于FP，直接将参数初始化为$A^{kNN}$即可；对于MLP-$k$NN，将MLP初始化为单位矩阵即可。MLP-$k$NN的两种变体：（1）MLP：$d’\equiv d$；（2）MLP-D：参数矩阵是对角矩阵，其他元素为0。

邻接关系处理器

设生成器输出的邻接矩阵为$\tilde{A}$，那么

$$A=\frac{1}{2}D^{-1/2}(P(\tilde{A})+P(\tilde{A})^T)D^{-1/2}$$

其中$P$是一个函数，取值范围为非负数。$A$保证了对称性和元素的非负性。

分类器

分类器：$\mathbb{R}^{n\times d}\times \mathbb{R}^{n\times n}\to \mathbb{R}^{n\times |C|}$取节点特征$X$和生成的邻接矩阵$A$作为输入，输出节点的类别标签。分类器的训练损失为交叉熵$\mathcal{L}_C$。

自监督

作者发现单独的交叉熵分类损失会导致生成的邻接矩阵中包含一些随机的边，因为这些边是否存在不会对半监督的交叉熵损失造成影响。同时在基准数据集上，这些随机边的比例较高。 于是，作者额外加入一个去躁自编码器DAE预测节点特征。

最终的损失函数定义为$\mathcal{L}=\mathcal{L}_C+\mathcal{L}_{DAE}$。SUBLIME在对比SLAPS时，无监督的条件下只使用$\mathcal{L}_{DAE}$。

Diffusion Improves Graph Learning

论文链接： ( , & al., , & (). Diffusion Improves Graph Learning. https://doi.org/10.48550/arXiv.1911.05485 ) ，实际发表于NIPS2019，作者在2022年又在arXiv上传了一个新版本。

Diffusion是一种图结构增强的方法。本文主张使用增强后的图结构输入现有模型，而 ( & , & (). Contrastive Multi-View Representation Learning on Graphs. https://doi.org/10.48550/arXiv.2006.05582 ) 将原图和diffusion后的图作为两个视角进行多视角学习。

广义图扩散：$S=\sum_{k=0}^{\infty}\theta_k T^k$，其中$\theta_k$和$T^k$的选择需要确保该级数是收敛的。 本文使用了更严格的条件，即要求$\sum_{k=0}^{\infty}\theta_k=1,\theta_k\in[0,1]$，且$T$的特征值$\lambda_i\in[0,1]$。这两个要求是$S$收敛的充分条件。 $T$称为转移矩阵。

  • 转移矩阵：转移矩阵可以选择随机游走转移矩阵$T_{rw}=AD^{-1}$和对称转移矩阵$T_{sym}=D^{-1/2}AD^{-1/2}$，其中$D_{ii}=\sum_{j=1}^NA_{ij}$表示度矩阵。$T_{rw}$是列随机矩阵（column-stochastic），即每一列的求和等于$1$。进一步地，可以定义

$$\tilde{T}_{sym}=(w_{loop}I_N+D)^{-1/2}(w_{loop}I_N+A)(w_{loop}I_N+D)^{-1/2}$$

其中$w_{loop}\in\mathbb{R}^+$，表示随机游走以$p_{stay,i}=w_{loop}/D_i$停留在$i$节点。

  • 扩散的例子：两个常用的图扩散是Personalized PageRank（PPR）和热核（the heat kernel）。

    • PPR: $T=T_{rw}$，$\theta_k^{PPR}=\alpha(1-\alpha)^k$，$\alpha\in(0,1)$
    • 热核：$T=T_{rw}$，$\theta_k^{HK}=e^{-t}\frac{t^k}{k!}$
    • 近似图卷积：$T=\tilde{T}^{sym}$，$w_{loop}=1$，$\theta_1=1,\theta_k=0,\forall k\neq 1$

  • 稀疏化：$S$通常是稠密的。可以用top-$k$或$\epsilon$-阈值法剔除$S$中的部分元素。