最近发现一篇ICLR2023 spotlight的蒸馏GNN到MLP的论文 ( , & al., , , , & (). NOSMOG: Learning Noise-robust and Structure-aware MLPs on Graphs. https://doi.org/10.48550/arXiv.2208.10010 ) ，觉得很新鲜。向前追溯发现其是基于ICLR2022的GLNN ( , & al., , , & (). Graph-less Neural Networks: Teaching Old MLPs New Tricks via Distillation. https://doi.org/10.48550/arXiv.2110.08727 ) 做的，遂在这里整理一下相关内容和自己的理解。

Graph-less Neural Networks (GLNN)

作者 ( , & al., , , & (). Graph-less Neural Networks: Teaching Old MLPs New Tricks via Distillation. https://doi.org/10.48550/arXiv.2110.08727 ) 指出现实场景难以落地GNN的一大原因是GNN的推理速度很慢。假设图中平均的顶点度为$R$，那么对于一个$L$层GNN的网络，总共需要提取(fetch)$O(R^L)$次邻居和自己的节点特征。如下图所示。该指数量级的提取次数导致GNN的推理时间随层数增加而指数上升。 另一方面，多层感知机MLP由于不需要图结构作为输入，因此无需提取其他节点的特征，推理速度是线性的。

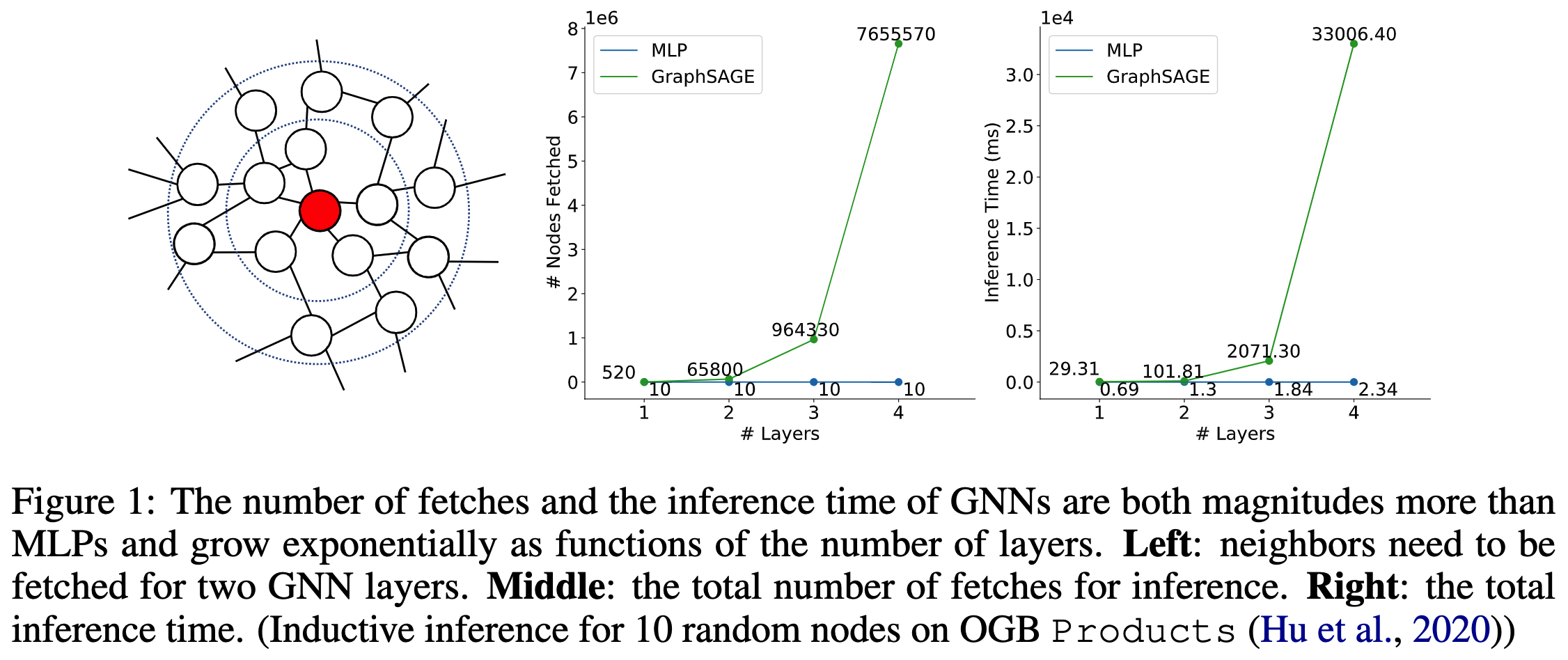
为了节省推理时间，直接使用MLP在图上训练也是不可行的，因为丢掉了图结构信息。为了达到MLP的推理时间同时尽量保留图的结构信息，作者提出了从GNN蒸馏知识到MLP的方法，并验证了其有效性。

解决框架

GLNN的结构容易理解，先训练一个笨重的GNN模型作为教师模型，再使用该GNN的输出$\mathbf{z}_v$以及带标签节点本身的标签$\mathbf{y}_v$训练简单的MLP学生网络。在归纳式学习(inductive learning)场景中， 当新的节点到来时，不再考虑其与训练图结构的连边，而是直接输入到MLP中做推理。 如下图所示。

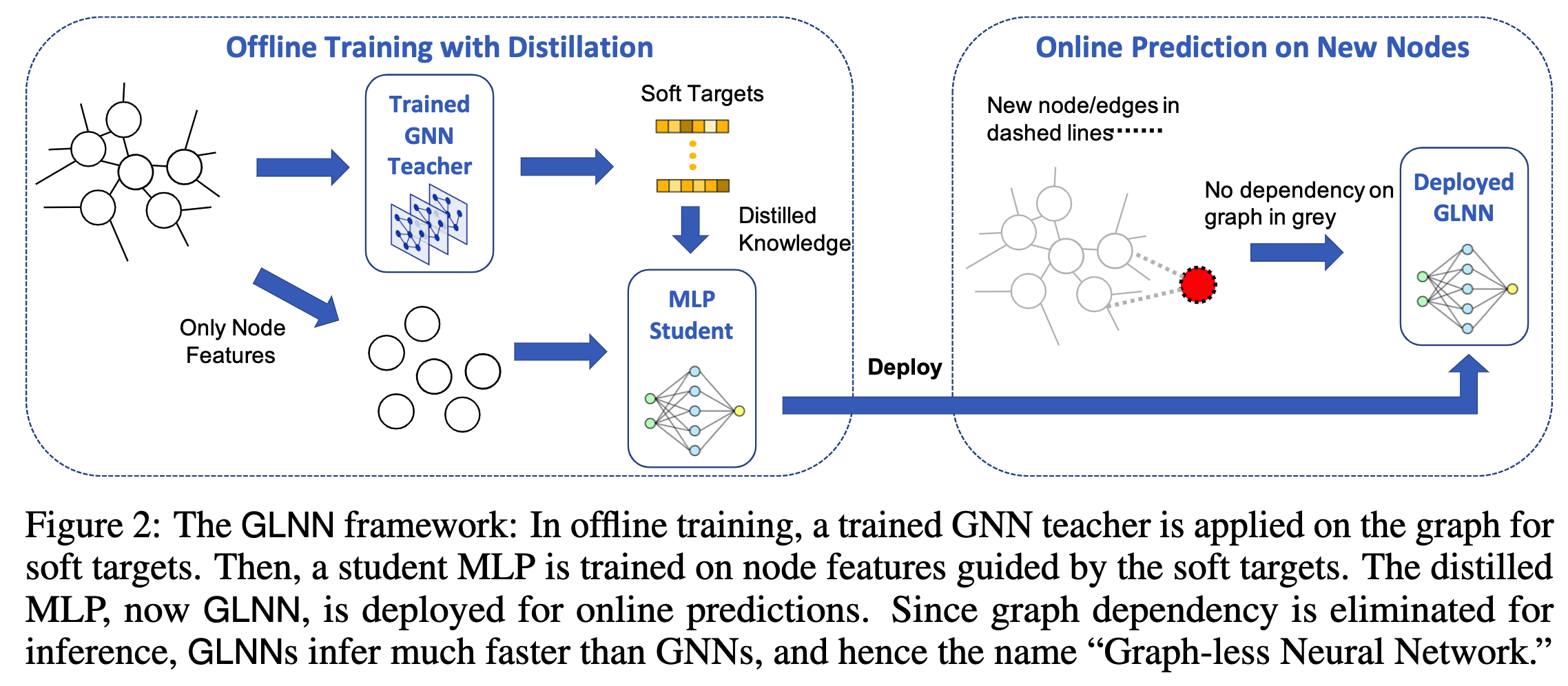
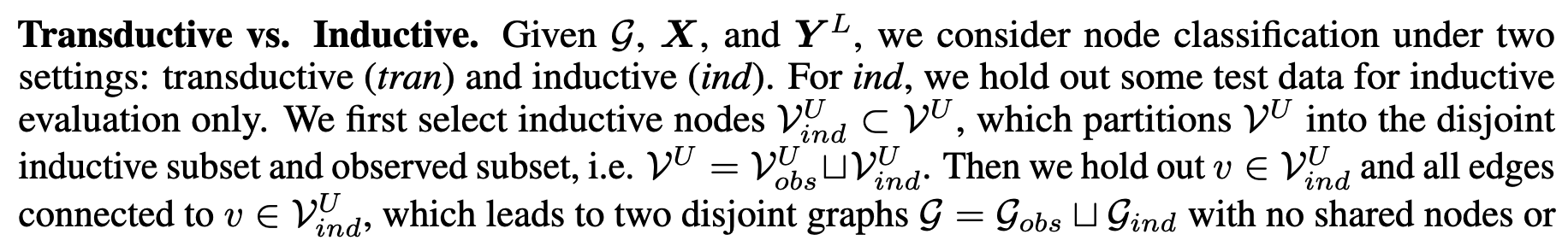
作者对于直推式和归纳式的详细描述： 可以看到测试时MLP和GLNN的学生网络是没有图结构输入的，只有测试顶点的特征向量。 同时，在测试教师网络GNN的归纳式推理时，只使用训练集图结构训练，而在测试时使用了包括测试顶点在内的整张图作为输入。这样对比是公平的。因为在使用GNN模型推理时我们会尽可能发挥模型的性能，为模型提供尽可能多的信息（见代码 official code）。

训练学生网络时使用的损失函数为

$$\mathcal{L}=\lambda\sum_{v\in\mathcal{V}^L}\mathcal{L}_{label}(\hat{\mathbf{y}}_v,\mathbf{y}_v)+(1-\lambda)\sum_{v\in\mathcal{V}}\mathcal{L}_{teacher}(\hat{\mathbf{y}}_v,\mathbf{z}_v)$$

其中$\mathcal{L}_{label}$为交叉熵损失，$\mathcal{L}_{teacher}$为KL散度损失，$\lambda\in[0,1]$是超参数，$\mathcal{V}^L$表示带标签的训练节点，$\mathcal{V}$表示所有训练节点。$\mathcal{L}_{teacher}$的含义是使学生网络输出的分布与教师网络的输出分布相近。

实验

作者做了大量的实验，包括直推式(transductive)的推理、归纳式(inductive)的推理，与其他GNN加速方法做了比较，通过一个参量(min-cut loss)验证蒸馏的有效性，验证GLNN的表达能力(理论推导)，分析了GLNN失败的场景。参数实验（消融实验）中验证了特征中加噪声的影响，归纳式推理时不同训练测试划分的影响，以及使用其他教师网络模型的情况。在附录部分还加了在异配图（NON-HOMOPHILY）上的实验，并更加详细地分析了节点特征噪声对GLNN的影响。

作者指出虽然现实场景中大多是归纳式推理，但直推式推理的实验仍然是有意义的(附录A.5)。第一，大多数现有GNN文献使用的是直推式的推理，为了公平对比。第二，直推式推理相对简单，因为在训练时看到了测试节点的特征。只有直推式能够work才能接着考虑更有挑战性的归纳式推理。第三，因为半监督训练时使用的标签很少，如pubmed数据集只有每个类别20个共60个标签，作者希望尽可能使用更多无标签节点提升性能。在现实场景中，当有很多无标签节点需要推理时，同样可以把它们拿来训练，然后用另一组不同的带标签测试节点做评测。

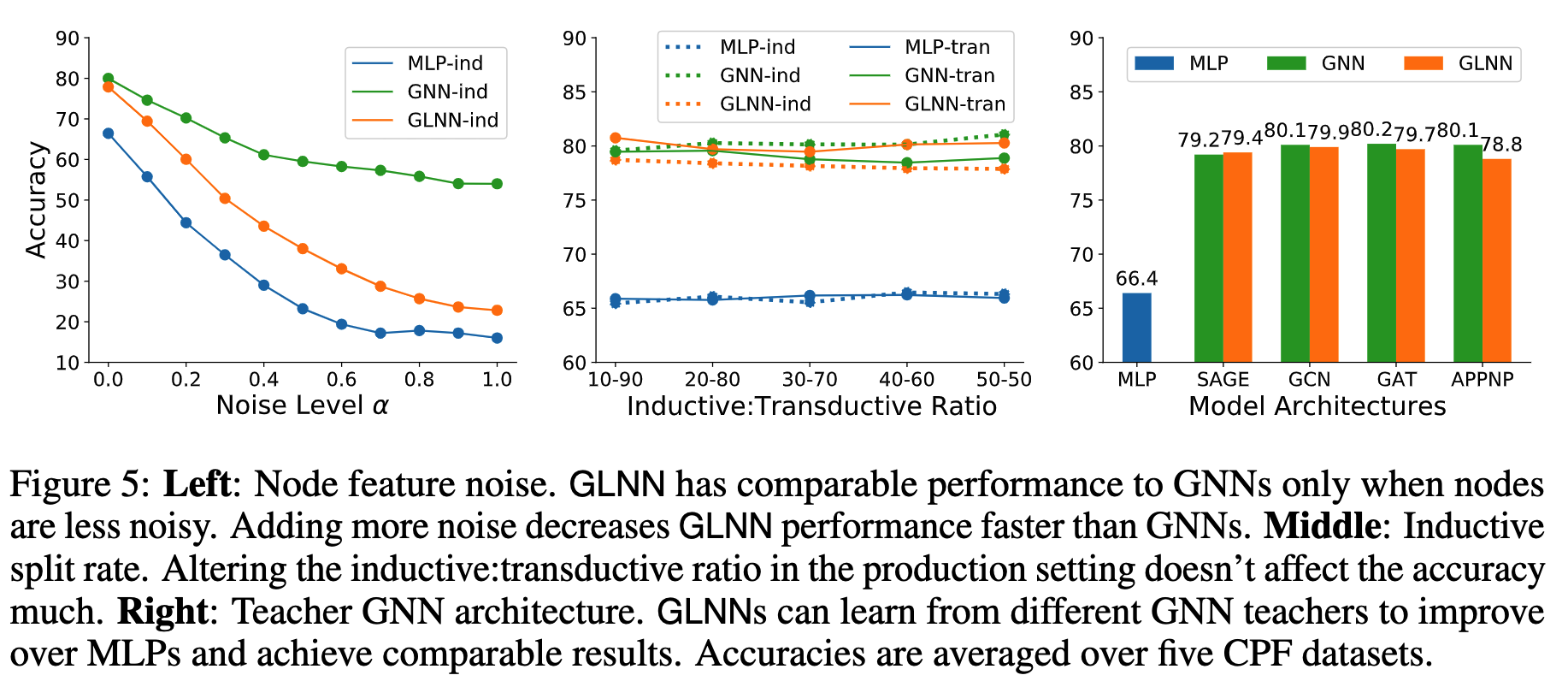
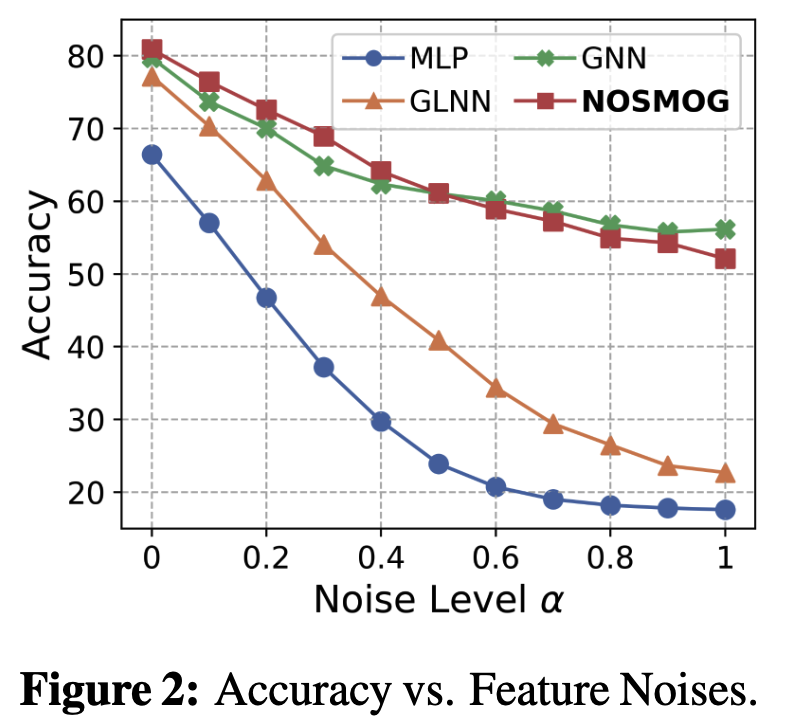
在附录J中，作者详细讨论了使用噪声扰动节点特征的实验结果(如下图Left)。发现2点：

  1. 当节点特征为纯高斯噪声($\alpha=1$)时，原始GNN仍然相对较好；
  2. 当节点特征为纯高斯噪声($\alpha=1$)时，蒸馏的GLNN比纯训练MLP好。

觉得这两个结果特殊是因为作者在正文5.8简单分析了什么情况下GLNN会失效，通过互信息：

$$I(G;y_i)=I(X^{[i]},\mathcal{E}^{[i]};y_i)=I(\mathcal{E}^{[i]};y_i)+I(X^{[i]};y_i|\mathcal{E}^{[i]})$$

最小化$\mathcal{L}_{label}$相当于在最大化$I(G;y_i)$。在上式中，$I(\mathcal{E}^{[i]};y_i)$表示边与节点标签的互信息，这是MLP无法访问到的。因此MLP只能最大化第二项$I(X^{[i]};y_i|\mathcal{E}^{[i]})$。然而，当节点的标签与特征无关时，比如节点的标签表示节点的度或者节点是否构成一个三角形，此时MLP和GLNN的学生网络都无法学到单单从节点特征到标签的映射$f$。这样分析的话上面的第2条实验结果就有点奇怪。

作者在附录J首先分析了为什么GNN在随机节点特征数据上仍然表现良好：过拟合。假设有一个A,B,C,D共4个顶点构成的全连接图(clique)，以及只与D相连的顶点E。令A,B,C,D的节点特征为纯高斯噪声，且具有相同的标签c。现在使用B,C,D,E训练GNN，A用作归纳测试。假设使用1层GNN。由于B,C,D内部的连边过于稠密，导致聚合邻居后B,C,D的表征十分地接近，而E对D的影响则十分小。因此模型会过拟合地将B,C,D的特征映射到标签c。当使用A做测试时，同样的聚合操作导致A与B,C,D十分接近，因此会输出相同的标签c，从而导致分类正确（GNN归纳式推理时使用全部邻接矩阵作为输入）。总的来说，如果A与许多具有相同标签的训练邻居稠密连接，那么就可能训练出一个过拟合的分类器，直接将其映射到相同的标签。

第二分析了为什么GLNN的学生网络好于MLP：测试集标签的不平衡。按照现有的训练/测试集划分，训练集的节点标签是均衡的，而测试集可能是不均衡的。结果是，MLP的预测也相对均衡，而GLNN可以从教师网络的soft labels中学习，因此GLNN的预测标签分布与真实的不平衡标签分布更加相似。如下图所示。

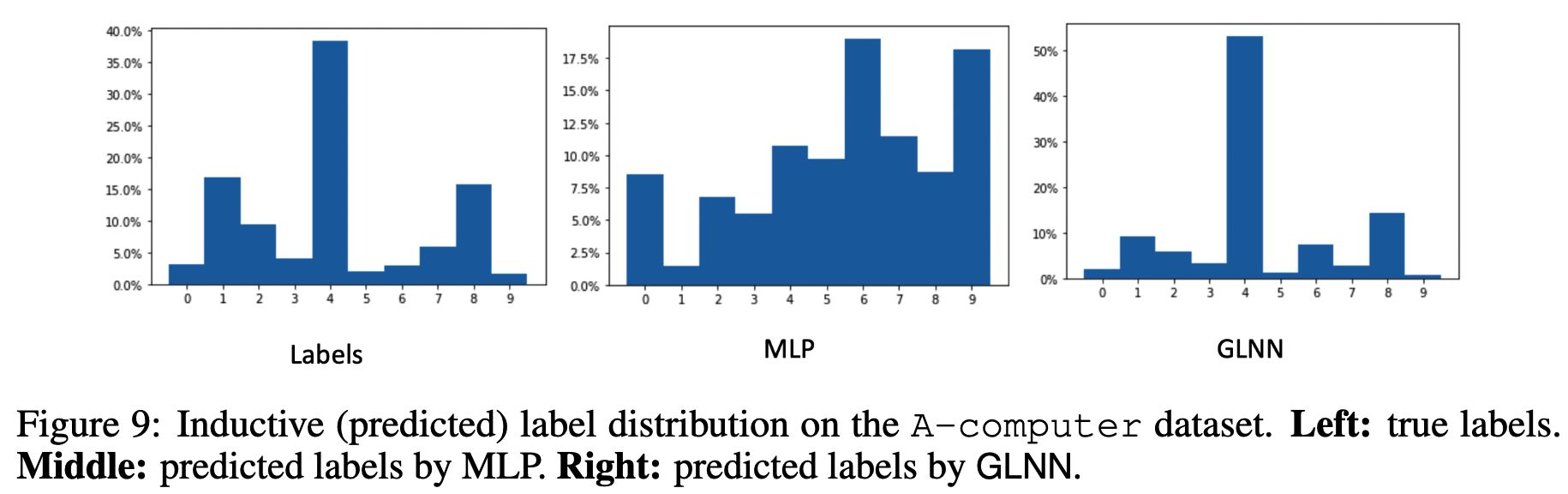
NOise-robust Structure-aware MLPs On Graphs (NOSMOG)

解决的问题和框架基本和GLNN相同，作者 ( , & al., , , , & (). NOSMOG: Learning Noise-robust and Structure-aware MLPs on Graphs. https://doi.org/10.48550/arXiv.2208.10010 ) 针对GLNN存在的不足进行优化。两大卖点是标题中的对噪声的鲁棒和对图结构的感知。使用对抗学习解决噪声的干扰，效果如下图：

image

扩展

  • GLNN 文中一个重要的结论是，对于现实中的属性图数据集，使用与GNN相同的参数量，存在一组MLP的参数，由节点的特征向量映射到其类别标签而取得与GNN相近的准确率，只是单单使用MLP以及标准的随机梯度下降难以学习到这样的参数 (5.3节、5.6节)。这表明节点的特征向量本身具有足够多的信息。这启发了后续KDD2022的GraphMAE ( , & al., , , , , , & (). GraphMAE: Self-Supervised Masked Graph Autoencoders. https://doi.org/10.48550/arXiv.2205.10803 ) 构建重构特征的图自编码器。
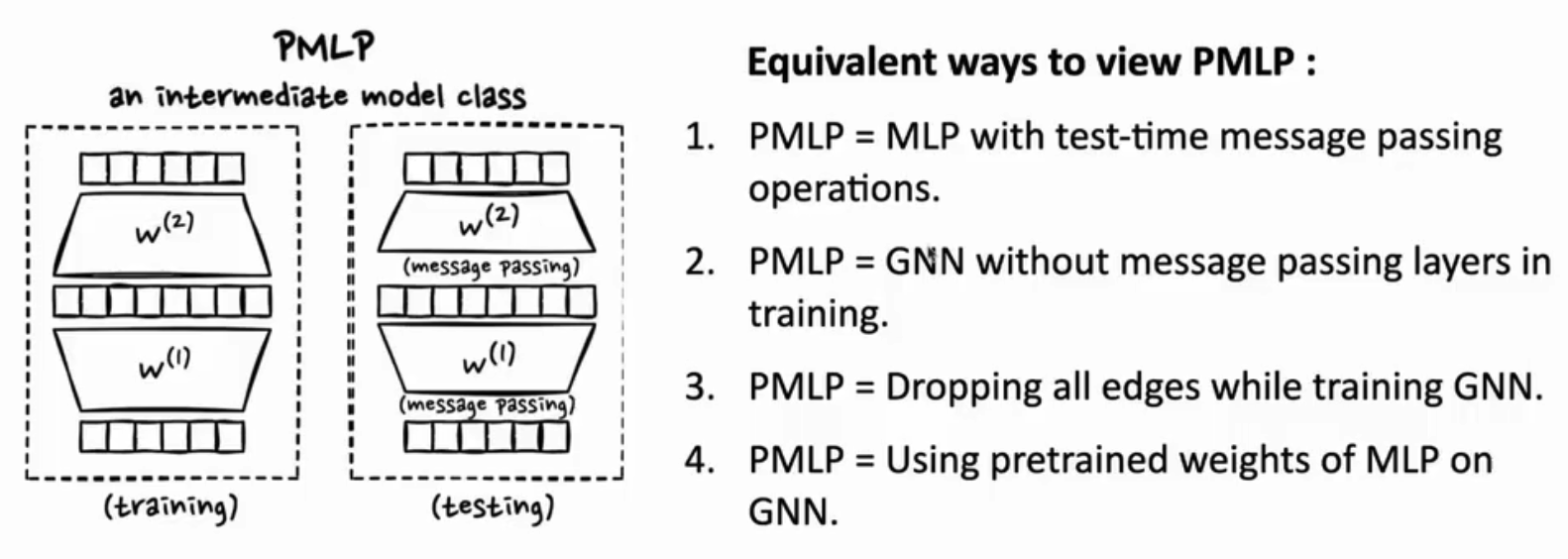
  • ICLR2023 还有一篇联系GNN与MLP的文章 ( , & al., , , & (). Graph Neural Networks are Inherently Good Generalizers: Insights by Bridging GNNs and MLPs. https://doi.org/10.48550/arXiv.2212.09034 ) 。与GLNN不同，PMLP ( , & al., , , & (). Graph Neural Networks are Inherently Good Generalizers: Insights by Bridging GNNs and MLPs. https://doi.org/10.48550/arXiv.2212.09034 ) 在训练时采用MLP架构，而在测试时重新添加信息传递(message passing, MP)操作，同样取得了与GNN相近的准确率。测试时MP添加的位置和次数可以自主设定。作者在与不同的原始GNN架构对比时使用了不同的PMLP测试架构。如下图所示 (来源于作者的报告: bilibili)。
  • 还有研究者整理了近期GNN&MLP的论文在Github。

References

Tian, Zhang, Guo, Zhang & Chawla (2023)
, , , & (). NOSMOG: Learning Noise-robust and Structure-aware MLPs on Graphs. https://doi.org/10.48550/arXiv.2208.10010
Hou, Liu, Cen, Dong, Yang, Wang & Tang (2022)
, , , , , & (). GraphMAE: Self-Supervised Masked Graph Autoencoders. https://doi.org/10.48550/arXiv.2205.10803
Yang, Wu, Wang & Yan (2023)
, , & (). Graph Neural Networks are Inherently Good Generalizers: Insights by Bridging GNNs and MLPs. https://doi.org/10.48550/arXiv.2212.09034
Zhang, Liu, Sun & Shah (2022)
, , & (). Graph-less Neural Networks: Teaching Old MLPs New Tricks via Distillation. https://doi.org/10.48550/arXiv.2110.08727