本文是 ( Citation: Xu, Zhang & al., 2021 Xu, K., Zhang, M., Li, J., Du, S., Kawarabayashi, K. & Jegelka, S. (2021). How Neural Networks Extrapolate: From Feedforward to Graph Neural Networks. https://doi.org/10.48550/arXiv.2009.11848 ) 的论文解读。OpenReview显示这篇论文是ICLR2021的Oral论文(前5%)。
引言
人类具有泛化性,例如学会算术后可以应用到任意大的数字。对于神经网络而言,前馈网络(也叫多层感知机,MLPs)在学习简单的多项式函数时就不能很好地泛化了。然而,基于MLP的图神经网络(GNNs)却在近期的一些任务上表现出较好的泛化性,包括预测物理系统的演进规律,学习图论算法,解决数学公式等。 粗略地分析可能会觉得神经网络可以在训练分布以外的数据上有任意不确定的表现,但是现实中的神经网络大多是用梯度下降训练的,这就导致其泛化性能有规律可以分析。作者使用"神经切线核"(neural tangent kernel,NTK)工具进行分析。
本文的第一个结论是使用梯度下降训练的MLPs会收敛到任意方向线性的函数,因此MLPs在大多数非线性任务上无法泛化。
接着本文将分析延伸到基于MLP的GNNs,得到第二个结论:使用线性对齐简化目标函数使得基于MLP的GNNs在非线性任务上能够泛化,即将非线性部分提前集成在模型的结构(如GNN的聚合和读出函数)或在输入的表征向量中(使用无监督方法将输入特征转化为表征向量)。
前置知识
设$\mathcal{X}$表示数据(向量或图)的域。任务是学习一个函数$g:\mathcal{X}\to \mathbb{R}$,其中训练数据$\{(\pmb{x}_i,y_i)\}\in\mathcal{D}$,$y_i=g(\pmb{x_i})$,$\mathcal{D}$表示训练数据的分布。在训练数据和测试数据同分布的情况下,$\mathcal{D}=\mathcal{X}$;而在评估泛化能力时,$\mathcal{D} $是$\mathcal{X}$的子集。一个模型的泛化能力可以用泛化误差评估:设$f$为模型在训练数据上得到的函数,$l$为任意损失函数,则泛化误差定义为$\mathbb{E}_{\pmb{x}\sim \mathcal{X} \setminus \mathcal{D}}[l(f(\pmb{x}), g(\pmb{x}))]$
图神经网络GNNs是在MLPs基础上定义的网络。具体来说,初始顶点表征为$\pmb{h}_u^{(0)}=\pmb{x}_u$。在第$k={1..K}$层,顶点表征更新公式为
$$\begin{aligned}\pmb{h}_u^{(k)}&=\sum_{v\in\mathcal{N}(u)}\text{MLP}^{(k)}(\pmb{h}_u^{(k-1)},\pmb{h}_v^{(k-1)},\pmb{w}_{(v,u)}) \\ \pmb{h}_G&=\text{MLP}^{(K+1)}(\sum_{u\in G}\pmb{h}_u^{(K)})\end{aligned}$$
其中$\pmb{h}_u^{(k)}$表示第$k$层GNN输出的顶点$u$的表征,$\pmb{h}_G$表示整张图的表征。$\pmb{h}_u^{(k)}$的计算过程称为聚合,$\pmb{h}_G$的计算过程称为读出。以往研究大多使用$\text{sum}$聚合与$\text{sum}$读出,而本文指出替换为另外的函数能够提升泛化性能。
前馈网络MLPs如何泛化
ReLU MLPs的线性泛化
作者用下图呈现MLPs的泛化方式。灰色表示MLPs要学习的真实函数,蓝色和黑色分别表示模型在训练集和测试集上的预测。可以看到模型可以拟合训练集上的非线性函数,但脱离训练集后迅速变为线性函数。用数字来说,脱离训练集后MLPs预测的决定系数大于$0.99$。

定理1(线性泛化):假设在NTK机制下使用均方误差训练了一个两层MLP:$f:\mathbb{R}^d\to\mathbb{R}$。对于任意方向$\pmb{v}\in\mathbb{R}^d$,令$\pmb{x}_0=t\pmb{v}$,那么当$t\to\infty$时,$f(\pmb{x}_0+h\pmb{v})-f(\pmb{x}_0)\to\beta_vh$对任意的$h>0$成立,$\beta_v$是常数。进一步地,给定$\epsilon>0$,对于$t=O(\frac{1}{\epsilon})$,$|\frac{f(\pmb{x}_0+h\pmb{v})-f(\pmb{x}_0)}{h}-\beta_v|<\epsilon$。
定理1说明了在训练数据集以外,ReLU MLPs可以拟合几乎线性的函数。对于二次函数($\pmb{x}^TA\pmb{x}$)、余弦函数($\sum_{i=1}^d\cos(2\pi\cdot\pmb{x}^{(i)})$)、根次函数($\sum_{i=1}^d\sqrt{\pmb{x}^{(i)}}$)等,ReLU MLPs不能泛化。 在合适的超参数下,MLPs可以正确地泛化L1范数,与定理1一致。如下图所示。

ReLU MLPs什么时候一定(provably)可以泛化
尽管上图显示MLPs对于线性函数可以较好地泛化,但这需要一定的条件,即训练数据集的分布必须足够“多样”。下面的引理1指出只需要$2d$条认真挑选的数据就可以实现ReLU MLPs的线性泛化。
引理1:令$g(\pmb{x})=\pmb{\beta}^T\pmb{x}$表示待拟合的目标函数,$\pmb{\beta}\in\mathbb{R}^d$。假设数据集$\{\pmb{x}_i\}_{i=1}^n$包含正交基$\{\hat{\pmb{x}}_i\}_{i=1}^d$和$\{-\hat{\pmb{x}}_i\}_{i=1}^d$。若使用均方误差在$\{({\pmb{x}}_i,y_i)\}_{i=1}^n$上训练一个两层ReLU MLP,那么$f({\pmb{x}})={\pmb{\beta}}^T{\pmb{x}}$对任意的${\pmb{x}}\in\mathbb{R}^d$成立。
然而,仔细挑选出$2d$条符合条件的样本并不容易。下面的定理2基于更现实的场景,指出只要训练数据的分布包含所有的方向(例如一个包含原点的超球),那么在足够的训练数据量下MLP能够收敛到线性函数。
定理2(泛化的条件):令$g(\pmb{x})=\pmb{\beta}^T\pmb{x}$表示待拟合的目标函数,$\pmb{\beta}\in\mathbb{R}^d$。假设$\{\pmb{x}_i\}_{i=1}^n$从域$\mathcal{D}$中采样,其中$\mathcal{D}$包含一个连通的子集$S$,满足对任意非零向量$\pmb{w}\in\mathbb{R}^d$,存在$k>0$使得$k\pmb{w}\in S$。若在NTK机制下,使用均方误差在$\{({\pmb{x}}_i,y_i)\}_{i=1}^n$上训练一个两层ReLU MLP,$f(\pmb{x})\xrightarrow{p}\pmb{\beta}^T\pmb{x}$在$n\to\infty$时成立,即$f$依概率收敛到$g$。
定理2说明了为什么数据集中“虚假”的相关性(真实不应存在的相关性)会损害模型的泛化性能,补充了因果推理的论点。例如,如果人工收集的训练图片中只有在沙漠中的骆驼,这里骆驼和沙漠就是数据集不够“多样”导致的虚假相关性,实际上骆驼还生活在草原等多种环境上。那么此时定理2的条件不再满足,模型也可能因此不能很好地泛化。
总的来说,定理1指出MLPs对于大多数非线性函数不能泛化,定理2指出MLPs当训练数据足够多样时能够在线性目标函数下泛化。
使用其他激活函数的MLPs
以上讨论都基于使用ReLU激活函数的MLPs。除了ReLU,还有$\tanh(x),\cos(x),x^2$等激活函数。作者发现,在激活函数和待拟合的目标函数相近时,MLPs的泛化性能较好。
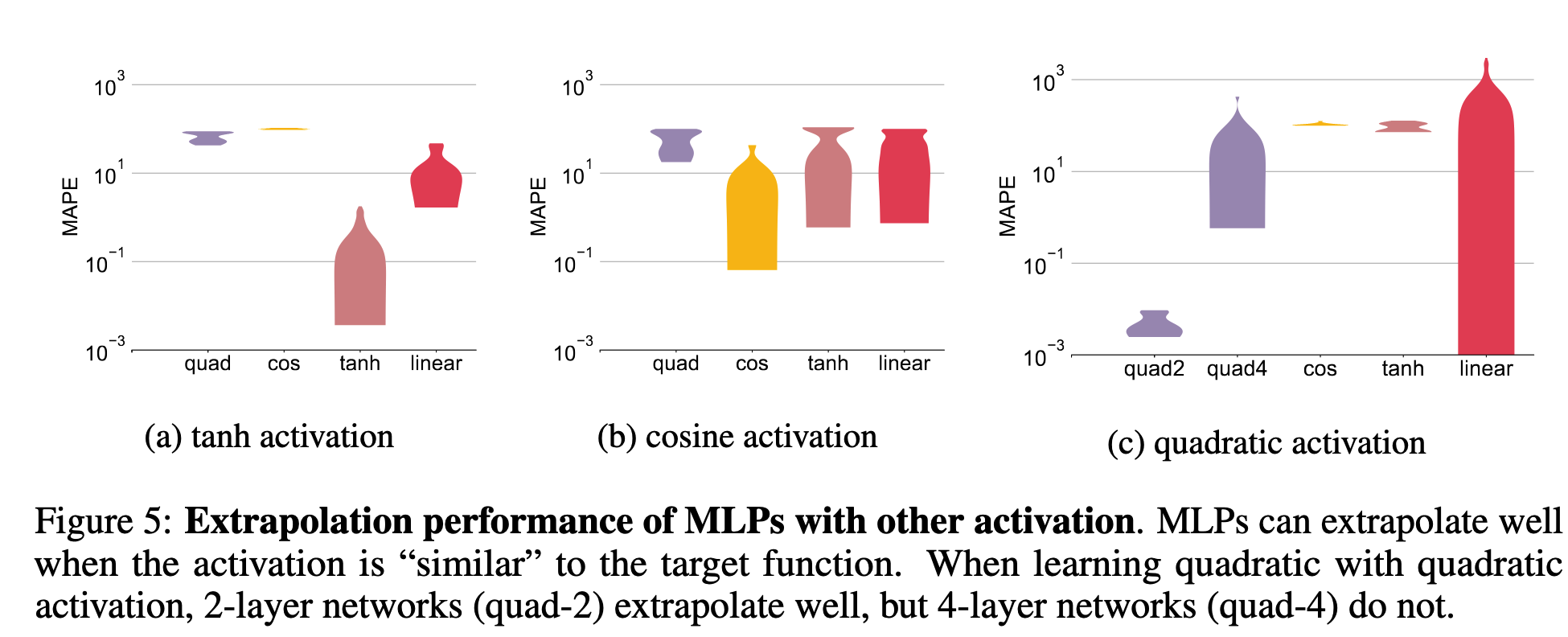
图神经网络GNNs如何泛化
以上讨论说明了MLPs在非线性任务上难以泛化。然而基于MLPs的GNNs却在一些非线性任务上表现出良好的泛化性,例如直观物理(intuitive Physics)、图论算法(graph algorithms)、符号数学(symbolic mathematics)等。
一个假设:线性对齐辅助了GNNs的泛化
GNNs可以被用来解决最短路径问题。人们发现在GNN的聚合函数中使用最小$\min$函数后,训练后的GNN可以较好地泛化到比训练集更大的图上:
$$\pmb{h}_u^{(k)}=\min_{v\in\mathcal{N}(u)}\text{MLP}^{(k)}(\pmb{h}_u^{(k-1)},\pmb{h}_v^{(k-1)},\pmb{w}_{(v,u)})$$
另一方面,传统的最短路问题可以通过Bellman-Fold(BF)算法解决:
$$d[k][u]=\min_{v\in\mathcal{N}(u)}d[k-1][v]+\pmb{w}(v,u)$$
其中$\pmb{w}(v,u)$表示边$(v,u)$的权重,$d[k][u]$表示$k$步以内到达节点$u$的最短距离。可以发现BF算法的更新式子可以很容易地与GNN的更新式子对齐:只需令MLP学习一个线性函数$d[k-1][v]+\pmb{w}(v,u)$即可。由于MLPs可以较好地对线性目标函数泛化,所以GNNs可以在计算最短路径问题上良好地泛化。 反之,如果在GNN的聚合函数中使用$\text{sum}$或其他函数,那么MLP就需要学习一个非线性目标函数,导致其无法泛化(定理1),进而导致GNN无法泛化。
由上述最短路问题推广到其他问题,作者发现许多GNNs泛化性能好的问题都可以用动态规划(dynamic programming, DP)解决,而DP中的迭代更新式子与GNNs的特征聚合函数很相似。
定义3:动态规划方法可以被形式化为:
$$\text{Answer}[k][s]=\text{DP-Update}(\{\text{Answer}[k-1][s’],s’=1,\cdots,n\})$$
其中$\text{Answer}[k][s]$表示第$k$次迭代、状态为$s$的子问题的解。
假设1(线性算法对齐):令$f:\mathcal{X}\to\mathbb{R}$表示目标函数。$\mathcal{N}$是一个神经网络,包含$m$个MLP模块。假设存在$m$个线性函数$\{g_i\}_{i=1}^m$,使得替换$\mathcal{N}$中的MLP后,$\mathcal{N}$能够模拟$f$。那么对于给定的$\epsilon>0$,存在$\{(x_i,f(x_i))\}_{i=1}^n\subset\mathcal{D}\subsetneq\mathcal{X}$,使得在其上通过梯度下降和均方误差损失训练的$\mathcal{N}$得到的$\hat{f}$满足$\parallel\hat{f}-f\parallel<\epsilon$。
作者认为,模型的线性对齐不局限于GNNs。人们可以将非线性的操作集成在模型的结构或者输入的表征向量中,这样在梯度下降训练时,模型只需要学习一个线性函数,从而提高了泛化能力。 GNNs学习DP的迭代表达式是一个例子,另外的例子是在算术任务中使用log-and-exp编码来提高乘法的泛化性。 另外,在一些任务中可能变换输入表征更容易。具体来说,目标函数$f$可以拆解为
$$f=g\circ h$$
其中$h$是表征向量,$g$是更简单的目标函数,例如线性函数,这样模型就更容易学习和泛化。对于表征向量$h$,可以使用领域知识;或者表征学习方法,在测试域$\mathcal{X}\setminus\mathcal{D}$进行无监督地表征学习。例如,在自然语言学习中,预训练表征和使用领域知识的特征转化可以帮助模型在不同语种之间泛化。在计量经济学中,人类对于本质因素或特征的判断(领域知识)尤其重要,因为金融市场经常需要模型进行泛化外推。
理论推导和实验结果
作者在3个DP任务上验证假设:最大度、最短路和$n$-body问题。首先,考虑计算图的最大度,可以通过1步DP解决。作为定理1的一个推论,使用$\text{sum}$聚合函数的GNNs无法在该问题上良好泛化。
推论1:使用$\text{sum}$聚合和$\text{sum}$读出的GNNs在最大度问题上不能泛化。
利用假设1,为了实现线性对齐,将GNN的读出函数修改为$\max$函数。下面的定理3说明修改后的GNN能够良好地泛化。
定理3(GNNs的泛化):假设图中所有的顶点有相同的特征向量。令$g$和$g’$分别表示最大度和最小度函数。令$\{(G_i,g(G_i))\}_{i=1}^n$表示训练集。如果$\{(g(G_i),g’(G_i),g(G_i)\cdot N_i^{\max},g’(G_i)\cdot N_i^{\min})\}_{i=1}^n$通过线性变换能表示$\mathbb{R}^4$(是$\mathbb{R}^4$的一组基),其中$N_i^{\max}$和$N_i^{\min}$分别表示$G_i$中具有最大度和最小度的顶点的个数,那么一个一层的使用$\max$读出函数的GNN,通过在$\{(G_i,g(G_i))\}_{i=1}^n$上使用均方误差损失和NTK机制训练,能够学习到目标函数$g$。
定理3中的条件与定理2类似,都是在保证训练集的多样性,只不过这里是用图的结构(即最大度)的多样性,而定理2中是用数据集的“方向”。如果训练集中所有的图有相同的最大度或者最小度,例如训练集仅仅属于path、$C$-regular graphs(度为$C$的正则图)、cycle、ladder四种类型之一,那么定理3的条件就遭到破坏,相应的GNN也不能保证学习到目标函数。
作者通过实验验证定理3和推论1。作者发现在最大度任务上,使用$\max$读出函数的GNN确实比使用$\text{sum}$读出函数的GNN的泛化效果要好;在最短路任务上,使用$\min$读出函数的GNN也确实比使用$\text{sum}$读出函数的GNN要好(图(a))。 此外,在图(b)中,作者考虑第3个任务:$n$-body问题,即预测重力系统中$n$个物体随时间演变的规律。GNN的输入是完全图,每个顶点代表一个物体。顶点的特征由物体的质量$m_u$、在$t$时刻的位置$\pmb{x}_u^{(t)}$和速度$\pmb{v}_u^{(t)}$拼接而来。边特征设定为$0$。GNN的输出是在$t+1$时刻每个物体$u$的速度。真实的速度$f(G;u)$可以近似表示为
$$ \begin{aligned} f(G;u)&\approx\pmb{v}_u^t+\pmb{a}_u^t\cdot\text{d}t \\ \pmb{a}_u^t &= C\cdot\sum_{v\neq u}\frac{m_v}{\parallel\pmb{x}_u^t-\pmb{x}_v^t\parallel_2^3}\cdot(\pmb{x}_v^t-\pmb{x}_u^t) \end{aligned} $$
其中$C$是常数。为了学习$f$,GNN中的MLP需要学习一个非线性函数,因此难以泛化。为了简化MLP的学习任务,使用表征$h(G)$替换输入的顶点特征。具体来说,将边特征由$0$替换为
$$\pmb{w}_{(u,v)}^{(t)}=m_v\cdot\frac{\pmb{x}_v^{(t)}-\pmb{x}_u^{(t)}}{\parallel\pmb{x}_u^t-\pmb{x}_v^t\parallel_2^3}$$
这样MLP只需要学习一个线性函数,从而提高了泛化能力。如下图(b)所示。

作者还发现训练图的结构也会对GNN的泛化能力造成影响,不同的任务中GNN更“喜欢”不同结构的训练图。如下图所示。

本文与其他分布外问题设置的联系
领域自适应(domain adaptation)研究如何泛化到一个特定的目标域。典型的方法是在训练中加入目标域的无标签样本。
自监督学习(self-supervised learning)研究如何在无标签样本上进行训练。
不变模型(invariant models)研究如何在多种训练分布之间学习内在不变的本质特征。
分布鲁棒性(distributional robustness)研究在数据分布上进行微小的对抗扰动,并保证模型在扰动后依然表现良好。
总结
本文的核心思想是通过改进模型结构或者输入信息简化目标函数,从而提升泛化性能。 对于实际场景,真实的目标函数很可能是复杂且未知的,所以通过修改模型的结构达到提高泛化能力的方法可能不太容易。使用无监督表征方法改进输入的特征向量是不错的方法。