FlashAttention论文发表于Neurips2022，第一单位是斯坦福大学。

作者提出了一种使用更小代价计算self-attention的方法，并从理论上保证flash-attention给出的是精确的attention值，与现有的近似attention不同。作者指出现有方法专注于减少FLOPs，而本文专注于减少IO。

输入：$\mathbf{Q},\mathbf{K},\mathbf{V}\in\mathbb{R}^{N\times d}$

输出：$\mathbf{O}\in\mathbb{R}^{N\times d}$

标准self-attention：

$\mathbf{S}=\mathbf{Q}\mathbf{K}^T\in\mathbb{R}^{N\times N}$

$\mathbf{P}=\exp(\mathbf{S})$

$\mathbf{O}=\mathbf{PV}/l(S)$，$l$始终表示向量元素求和或矩阵按行求和。

Flash-attention的思路：分块在高速on-chip显存上增量式计算，避免平方空间的$\mathbf{S}$。

首先推导增量式的softmax函数：

对一个向量$\mathbf{x}$计算softmax：$\sigma(\mathbf{x})=\exp(\mathbf{x})/{\sum_i {\exp(\mathbf{x}_i)}}$

对两个向量的拼接$[\mathbf{x},\mathbf{y}]$计算softmax：$\sigma([\mathbf{x},\mathbf{y}])=[\exp(\mathbf{x}),\exp(\mathbf{y})]/(\sum_i\exp(\mathbf{x}_i)+\sum_j\exp(\mathbf{y}_j))$

设$l(\mathbf{x})=\sum_i\exp(\mathbf{x}_i)$，则$\sigma([\mathbf{x},\mathbf{y}])=[\exp(\mathbf{x}),\exp(\mathbf{y})]/(l(\mathbf{x})+l(\mathbf{y}))$

将$\mathbf{Q,O},l$分成$T_r$块，将$\mathbf{K,V}$分成$T_c$块，进行二重循环。

1
2
3
4

for j in 1...T_c:
  取出K_j和V_j
  for i in 1...T_r:
    取出Q_i,O_i和l_i

计算当前块内的self-attention，即：

$\mathbf{S}_{ij}=\mathbf{Q}_i\mathbf{K}_j^T$

$\mathbf{P}_{ij}=\exp(\mathbf{S}_{ij})$

$l_{ij}=\text{rowsum}(\mathbf{P}_{ij})$

$\mathbf{O}_i’=\mathbf{P}_{ij}\mathbf{V}_j$

然后需要对上一轮的$\mathbf{O_i}$和$l_i$进行更新，以d=1为例。

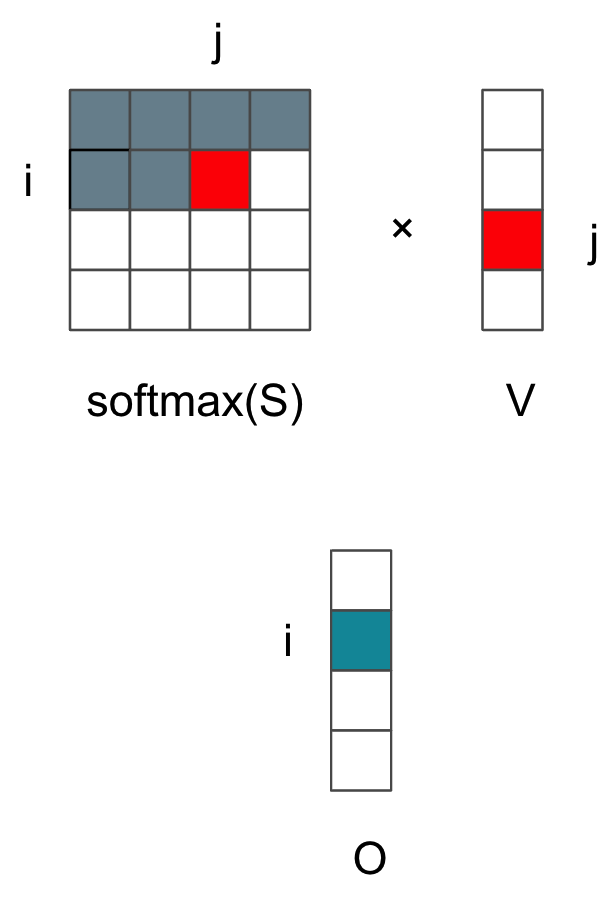
image

$l_i^{new}=l_i+l_{ij}$比较直接

两个红色的矩阵相乘得到当前的$\mathbf{O}_{ij}$。我们知道上一轮softmax使用的$l_i$只是当前i行的前部分之和，因此这里要乘以旧分母除以新分母，同时由于绿色$\mathbf{O}_i$由i行j列的内积得来，还需要加上$\mathbf{O}_{ij}$，这样得到$\mathbf{O}_i$的增量式更新：

$\mathbf{O}_i=\mathbf{O}_i*l_i/l_i^{new} + \mathbf{O}_{ij}$

论文中的Algorithm1由于考虑了算术稳定性防止\exp得到过大的值，在softmax前减去了最大值m，因此看起来更复杂。

发散QA

Q1. Algorithm 1中的i、j循环可以交换吗？github

A1. 如下可以，结果仍然保证Flash-Attention得到的是精确的$\mathbf{O}$。但显然增加了$\mathbf{K}_j$和$\mathbf{V}_j$的IO次数。

1
2
3
4
5
6
7
8

for i in 1...T_r:
  for j in 1...T_c:
    取出K_j和V_j
    取出Q_i,O_i和l_i

    ...

    更新O_i和l_i

如下不可以。

1
2
3
4
5
6
7
8

for i in 1...T_r:
  取出Q_i,O_i和l_i
  for j in 1...T_c:
    取出K_j和V_j
    
    ...
    
  更新O_i和l_i

Q2. $\mathbf{O}_i$的更新表达式怎么得来的？

A2. $\mathbf{O}_i=\mathbf{O}_i*l_i/l_i^{new} + \mathbf{O}_{ij}$。$\mathbf{O}_i$由$\mathbf{S}$的第i行的softmax和$\mathbf{V}$的第j列的内积得来。然而在这里分块计算时，softmax的分母，即对行的求和值$l$，是在不断更新的。只有到$\mathbf{S}$的i行最后一列时才得到正确的l，因此有这样的增量更新表达式。

同时，不按当前的算式更新，每次只累加softmax的分母，直到最后一列才除以$l$，肯定也是可以的。

References

[1] 我的flash-attention实现：awesome-papers/FlashAttention at main · yliuhz/awesome-papers (github.com)

[2] Flash Attention论文地址：https://doi.org/10.48550/arXiv.2205.14135